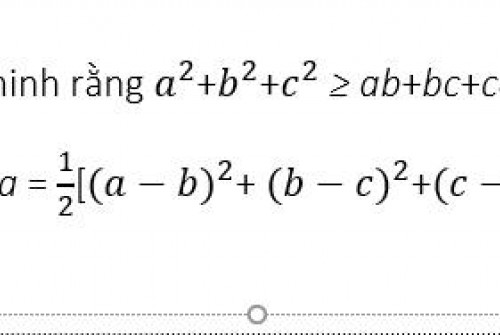Phương pháp đại số và đạo hàm

1. Phương pháp đại số:

Phương pháp đại số tập trung vào việc giải quyết các phương trình, bất phương trình, và hệ phương trình bằng cách sử dụng các phép biến đổi đại số như cộng, trừ, nhân, chia, và khai căn. Một số khái niệm cơ bản bao gồm:

• Phương trình bậc nhất, bậc hai (còn gọi là phương trình bậc hai có thể giải bằng công thức nghiệm hoặc hoàn thành bình phương).
• Hệ phương trình có thể được giải bằng phương pháp thế, cộng đại số hoặc ma trận.

2. Phương pháp đạo hàm:

Đạo hàm là công cụ của giải tích, giúp đo lường sự thay đổi của một hàm số khi biến số thay đổi. Phương pháp này chủ yếu được sử dụng để:

• Tìm tốc độ thay đổi của hàm số tại một điểm (hệ số góc của tiếp tuyến).
• Tìm cực đại, cực tiểu và điểm uốn của hàm số.
• Giải quyết các bài toán liên quan đến tối ưu hóa.

Phương pháp đạo hàm bao gồm các quy tắc như:

• Đạo hàm của hàm số mũ, đa thức, hàm số lượng giác.
• Quy tắc chuỗi, quy tắc tích, và quy tắc thương trong đạo hàm.